Interval Inversions
Learn How Inversions Work According To The Rule of 9
In this tutorial we're going to learn what are interval inversions.
As a quick refresher, an interval is a distance between two notes, or pitches. Depending on that distance, we'll obtain different sounds and feelings.
Some intervals sound very stable while others are dissonant and unstable. This is the basic palette of a musician.
Basic Intervals Table
If we take the major scale and count each of its note from the root, we get the following intervals:
| Interval | Name | Half-Steps |
|---|---|---|
| C - C | Unison | 0 |
| C - D | Major Second | 2 |
| C - E | Major Third | 4 |
| C - F | Perfect Fourth | 5 |
| C - G | Perfect Fifth | 7 |
| C - A | Major Sixth | 9 |
| C - B | Major Seventh | 11 |
| C - C | Octave | 12 |
Half-steps are also called semitones and correspond to frets on the guitar. 1 half-step = 1 semitones = 1 fret.
Interval Types
By looking at the table below, we notice that computing intervals (so far) is like doing primary school math: we count the notes and get names like Second, Third, Fourth, Fifth, Sixth and Seventh.
The octave interval is a particular one because contains notes with the same names (C and C) but at different pitches (think the same note played with open string and at the 12th fret)
We can also notice the types of intervals: Perfect, Minor, and Major.
So far so good.
But what about intervals of 6 half-steps, 1 half-step, or 8 half-steps? They don't exist on the table.
Well, we have to know that we can also have Diminished and Augmented intervals.
The image below shows you the relationship between all the kinds of intervals:
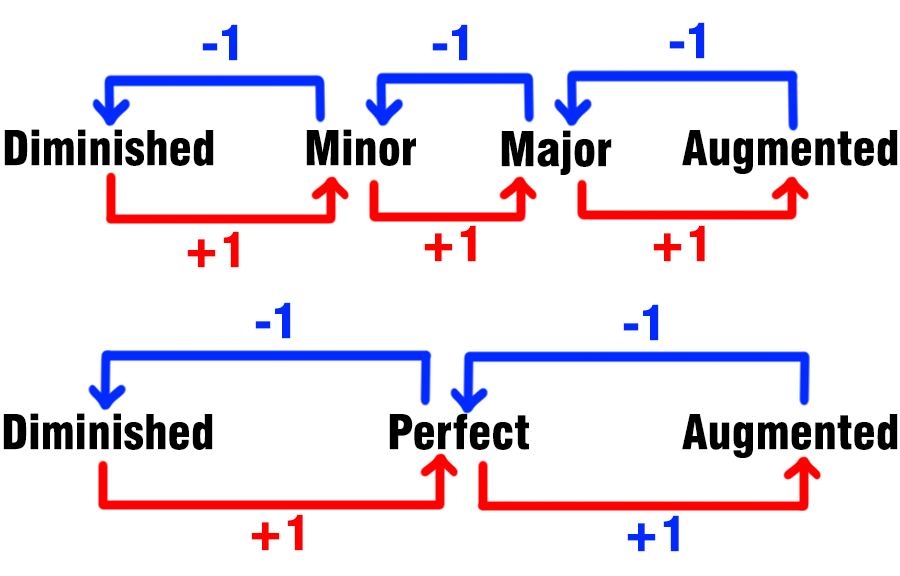
It works in this way:
- The Major Interval lowered by 1 half-step becomes a Minor Interval
- The Minor Interval, raised by 1 half-step, become a Major Interval
- The Perfect Interval, lowered by 1 half-step, becomes a Diminished Interval
- The Perfect Interval, raised by 1 half-step, becomes an Augmented Interval
- The Major Interval, raised by 1 half-step, becomes an Augmented Interval
- The Minor Interval, lowered by 1 half-step, becomes an Diminished Interval
Complete Interval Table
Now we can draw a complete table with all the intervals, with distances from 0 to 12.
| Interval | Example | Half-Steps | Symbol |
|---|---|---|---|
| Unison | (C-C) | 0 | 1 |
| Minor Second | (C-Db) | 1 | b2 |
| Major Second | (C-D) | 2 | 2 |
| Minor Third | (C-Eb) | 3 | b3 |
| Major Third | (C-E) | 4 | 3 |
| Perfect Fourth | (C-F) | 5 | 4 |
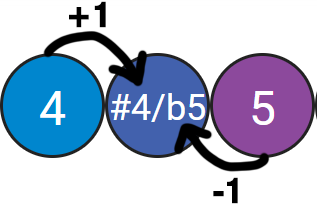
| Diminished Fifth / Augmented Fourth | (C-Gb)/(C-F#) | 6 | b5 |
| Perfect Fifth | (C-G) | 7 | 5 |
| Minor Sixth | (C-Ab) | 8 | b6 |
| Major Sixth | (C-A) | 9 | 6 |
| Minor Seventh | (C-Bb) | 10 | b7 |
| Major Seventh | (C-B) | 11 | 7 |
| Octave | (C-C) | 12 | 8 |
Did you see the row with "Diminished Fifth / Augmented Fourth"? What is this?
We can lower a Perfect Fifth by one half-step and get a Diminished Fifth ( 7 - 1 = 6), or we can raise a Perfect Fourth by one-half step and get an Augmented Fourth (5 + 1 = 6).
Same distance (6), but different names. This music theory strangeness is called enharmonics.
You can also use this fretboard intervals guide to play intervals on the guitar neck.
Interval Inversion
After this quick introduction, we are now ready to learn about interval inversion.
In an interval, an inversion happens when you move the lowest note to the higher octave, or, on the contrary, you move the highest note to the lowest octave.
For example, this is the interval A E (as always on guitar, it's helpful to show this concept on one single string), which is a Perfect Fifth (7 frets):

To get the inverted interval (E A), you can move the A one octave up, or you can move the E one octave below, as the picture below shows:

E A is five half-steps or frets, so it's a Perfect Fourth.
The Rule Of 9
Now it's time to unveil the rule that stays at the foundation of interval inversion: the rule of 9.
The rule of 9 says: the number of any interval and the number of its inversion always add up to nine.
In the example above, we inverted the 5th interval and we got the 4th interval, so 5+4 = 9
Here are other examples:

C-E is a Major Third (4 half-steps), its inversion, E-C, is a Minor Sixth (8 half-steps): 3+6=9

D-E is a Major Second (2 half-steps), E-D is a Minor Seventh (10 half-steps), 2+7=9
We could even think about the rules of 12: the sum of the half-steps in an interval and the half-steps in its inversion always add up to 12 (one octave).
What Happens To Interval Type During Inversion?
You might be wondering how the process of inversion impacts the type of interval. Here's a recap schema:
- When inverted, the Major interval becomes Minor
- The Minor interval becomes Major
- The Perfect interval remains Perfect
- The Diminished interval becomes Augmented
- The Augmented interval becomes Diminished
A Peculiar Interval: The Tritone
The Tritone is an interval 6 half-steps wide. It can have 2 names: Augmented fourth or Diminished Fifth.
The inverted interval of an Augmented Fourth is a Diminished Fifth, and vice-versa. Again, 4+5=9, or 5+4=9.
The particular characteristic of this interval is that it divides exactly the octave in 2 equal parts (12/6=2), and it's the most dissonant interval.
This ends our tutorial on interval inversions. To stay updated and get free access to the free resources, subscribe here.