The Circle of Fifths Made Easy (but incredibly useful)
Why and How to Use the Circle of Fifths + Interactive Learning Tool
This tutorial is a companion resource for the Interactive Circle Of Fifths Tool , a music learning software available on this site.
The Circle Of Fifths , also called Cof and Wheel of Fifths , was invented in the 1670s by Nikolai Diletskii in his "Grammatika"; this incredible device embeds all the music theory you need to know for doing a lot of funny things.
Indeed, at the end of this tutorial, you'll be able to use the Circle of Fifths to:
- Identify sharps and flats for each music key
- Know the chords that belong to a key
- Create chord progressions
- Modulate to other keys
- Transpose songs
- Create chords of different types
- Substitute chords
Don't feel overwhelmed by such an amount of information, the Circle of Fifths makes it easy to understand and master the tasks listed above.
Interactive Tool: You may want to open the Interactive Circle Of Fifths on a separate page so that you can follow this tutorial and experiment with the concepts with the tool.
Are you ready?
Let's unveil the hidden mysteries of the Circle Of Fifths!
Introduction
The Circle of Fifths is a geometric representation of how the 12 notes of the chromatic scale relate to one another.
If you look closely at the diagram you will see each note is a Perfect Fifth (seven semitones, or seven frets on the fretboard) higher than the next (going clockwise).
Not sure what is a Perfect Fifth? Then, before going forward, you should take a look at our tutorial on music intervals .
It will explain what intervals are and how to find them on the fretboard.
The G is a fifth away from the C in the major scale. Going clockwise on the Circle of Fifths the next note will always be a fifth away.
Now if we move counterclockwise on the Circle of Fifths, we are a fourth away, F is the fourth note of the C major scale.
So our clockwise sequence is:
- C
- G
- D
- A
- E
- B
- F#
- C#
- Ab
- Eb
- Bb
- F
- C
As always music theory can quickly get a little garbled which is why the Circle of Fifths is so very helpful.
It allows you to quickly see how each note in the scale relates to the next , and how it all falls into a convenient loop or circle.
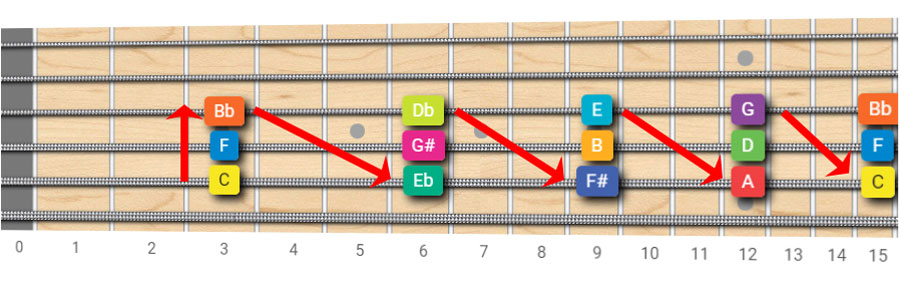
How To Memorize the Circle Of Fifths: Memory Trick for Guitar Players
Now here's a little trick for memorizing the Circle of Fifths with the help of the guitar fretboard.
If you know your guitar notes names , it will be easy to follow the Cof (Circle of Fifths) right on the neck.
We start from the C at the 3rd fret of the A string , and we go up by one Perfect Fifth, note after note.
With the help of fretboard octaves (again, if you don't know what octaves are, please go to the music intervals tutorial) our Circle Of Fifths can be laid out horizontally in the pattern shown below:
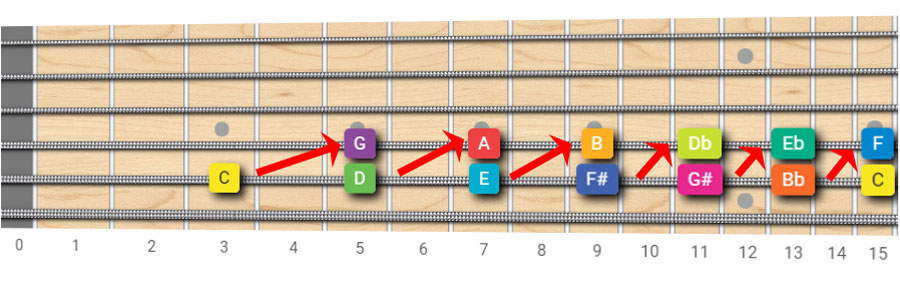
No need to memorize the Circle of Fifths if you know your fretboard notes!
Awesome!
We see that it's enough to learn this fretboard pattern for knowing the sequence of the notes in the Cof!
Just don’t forget that when we move:
- clockwise (left to right on the fretboard pattern), we are moving in fifths,
- counterclockwise , we are moving in fourths (right to left on the fretboard pattern)
Understanding enharmonics
Before approaching sharps and flats, We need to clarify what enharmonics are.
If you are already familiar with the subject, feel free to skip this section.
In western music, there are 12 notes in the chromatic scale, each one a semitone away from each other.
On your guitar, each fret represents one of these notes and every fret is one semitone.
These notes in the chromatic scale are;
- C
- C#/Db
- D
- D#/Eb
- E
- F
- F#/Gb
- G
- G#/Ab
- A
- A#/Bb
- B
- and then back to C
The notes with a slash are known as enharmonic notes , and they are the same pitch as each other. For example, C# is enharmonically equivalent to Db they are just spelled differently.
Depending on which key you are in will determine the spelling.
If you are in the key of E then you will spell the note C#, if in the key of Ab then you will spell the note as Db.
Now, of course, this can cause some immediate confusion, which is why we have the Circle of Fifths.
How to use the Circle of Fifths to organize music keys
The Circle of Fifths packs an awful lot of data into a small circle.
On the outside are the names of the major keys while on the inside are the names of the minor keys.
As we mentioned above the key of G is five steps above the key of C, and just as well the key of Em is five steps above the key of Am.
(If you use your fingers to count each note alphabetically you will see they each interval adds up to five).
How to find Sharps and flats
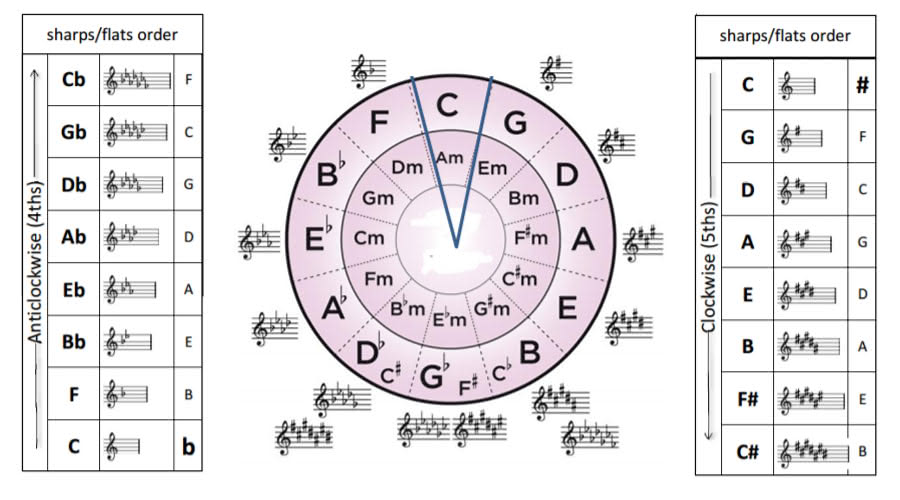
Sharps and flats in the CoF
The CoF also will denote how many sharps or flats are in each key. The sharps are on the right side and the flats on the left.
Starting at the top with C we have no sharps or flats as there are none in the C major scale.
From there each fifth adds another sharp, until we reach the bottom and then it goes backward with flats until we come back to C again.
Now you will notice at the bottom of the CoF that some keys have different spellings and can either be denoted with sharps or flats.
Remember from above that these are enharmonically equivalent it just depends on which the composer wishes to use.
If you are not sure how many sharps the Key of B has, well just count from the beginning of the CoF (excluding the natural key of C) and you will have five sharps.
If you want to know how many flats are in the enharmonic equivalent of B, which is Cb, well count backward and you will get 7 flats.
By knowing the number (if any) of sharps or flats, we will have the key signature readily available by the CoF.
Drill down: in my complete ebook, 52 Chord Progressions | Learn How To Connect Chords and Create Great Songs, you find the most common chord progressions used in Western Music, listed according the Circle Of Fifths
(As you read on keep checking back with the Circle of Fifths tool , that way you understand exactly what is written. The Cof is so wonderful because it simplifies all of this!).
You might want to check with a table with all major and minor keys.
Sharp keys: follow the CoF clockwise, one 5th at a time
| Key | Sharps | Notes |
|---|---|---|
| C | 0 | - |
| G | 1 | F# |
| D | 2 | F# C# |
| A | 3 | F# C# G# |
| E | 4 | F# C# G# D# |
| B | 5 | F# C# G# D# A# |
| F# | 6 | F# C# G# D# A# E# |
| C# | 7 | F# C# G# D# A# E# B# |
The sharps are added a 5th away from each other.
Notice that the new sharp is the root of the tonic one semitone below (G key, F#
Flat Keys: follow the CoF counterclockwise, one 4th at a time
| Key | Flats | Notes |
|---|---|---|
| F | 1 | Bb |
| Bb | 2 | Bb Eb |
| Eb | 3 | Bb Eb Ab |
| Ab | 4 | Bb Eb Ab Db |
| Db | 5 | Bb Eb Ab Db Gb |
| Gb | 6 | Bb Eb Ab Db Gb Cb |
| Cb | 7 | Bb Eb Ab Db Gb Cb Fb |
The flats appear a 4th away from each other
How to create chord progressions with the help of the Circle of Fifths
Now let’s work on building some chord progressions.
First a quick trick on how to find any major scale using the Cof.
To find the C scale we simply go counterclockwise one step and then count seven clockwise .
So one step counterclockwise is F and then counting forward C, G, D, A, E, and B.
And there you have the C major scale.
This works the same for every major scale, move back one and then up seven.
Of course after you find the right scale it helps to put it in order.
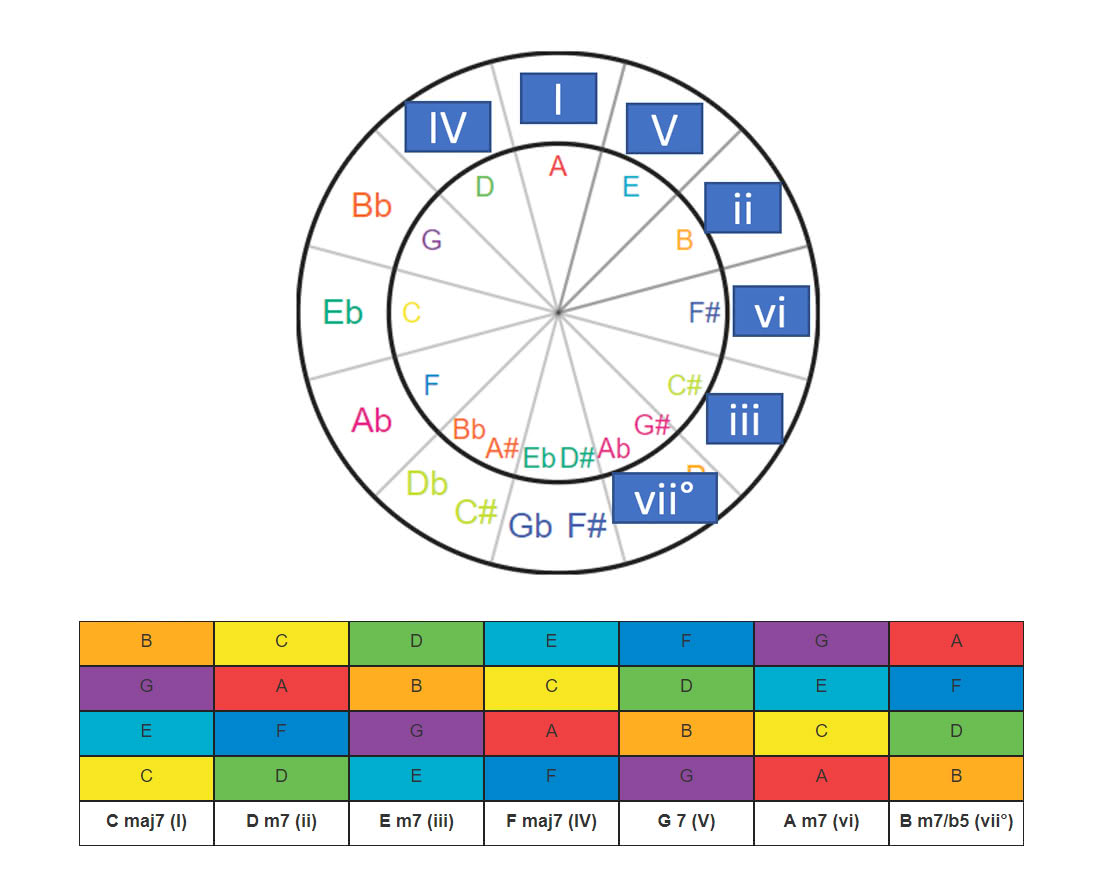
Chords Degrees
There are a few different methods to build chord progressions using the CoF. First though we need to remind ourselves of the Nashville Number System and Romand Numerals Notation .
It was devised as a way to show scale degrees to those musicians who knew little about music theory.
However, it turns out that it is also a handy system to teach said theory!
To find the chords of a key, just rotate the degrees
Major Scale Degrees
| Scale | I | ii | iii | IV | V | vi | vii° |
|---|---|---|---|---|---|---|---|
| Major | Major | Minor | Minor | Major | Major | Minor | Half-Diminished |
Minor Scale Degrees
| Scale | i | ii° | III | iv | v | VI | VII° |
|---|---|---|---|---|---|---|---|
| Minor | Minor | Half-Diminished | Major | Minor | Minor | Major | Major |
Chord Progressions
Now the numbers are written in Roman numerals so you will see a major key notated like;
- I
- ii
- iii
- IV
- V
- vi
- vii°
I-IV-V Chord Progression
 One of the most popular progressions ever in music is the
I-IV-V
or
the
1-4-5
, depending on how
it is shown. Since we have been dealing so exclusively with the key of C, let's change it up to
test our CoF knowledge.
One of the most popular progressions ever in music is the
I-IV-V
or
the
1-4-5
, depending on how
it is shown. Since we have been dealing so exclusively with the key of C, let's change it up to
test our CoF knowledge.
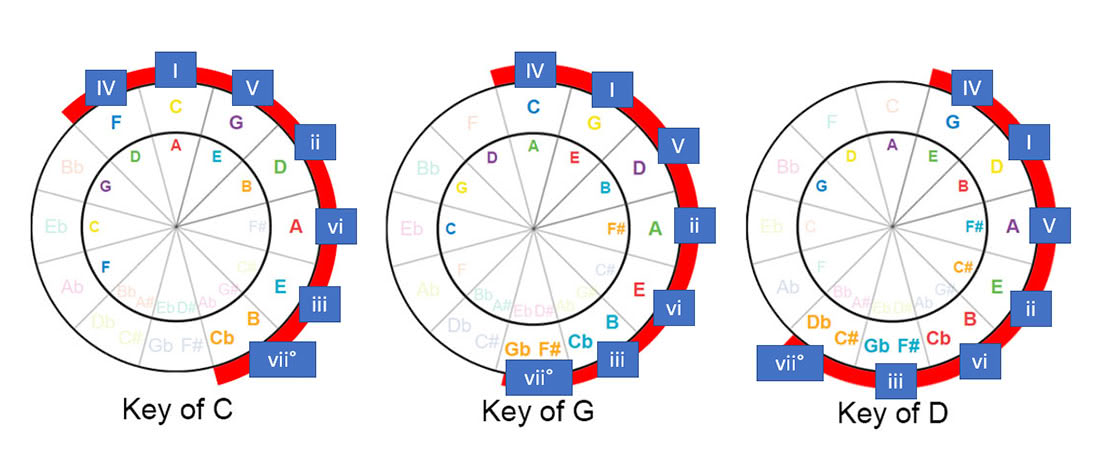
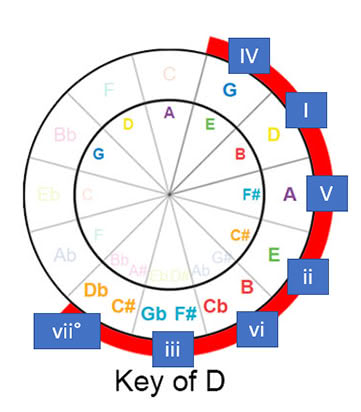
We will find the 1-4-5 progression for the key of D .
Remember when we move backward on the circle we move in fourths, forwards we move in fifths.
So if we look at D it’s easy to see the fourth behind it is G and the fifth in front is an A.
The 1-4-5 chords for the key of D is D-G-A .
If you happen upon a band jamming in 1-4-5 or I-IV-V all you need to know is the key and your CoF and you are golden.
Now here is another way to find your 1-4-5.
First find the D major scale, to find that we move one back and count forward seven;
G D A E B F# C# if we put it in order D E F# G A B C# and the 1-4-5 of this scale is again D-G-A.
I-V-vi-IV Chord Progression
This method helps if we want to find more complicated progressions.
Another super common pop music progression, called Four chord progression, is I-V-vi-IV or 1-5-6-4, so in the key of D that is D-A-Bm-G .
Doo Wop Chord Progression
Now try to find the Doo Wop progression I-vi-IV-V or 1-6-4-5 for the key of Eb.
One back and seven forward gets us;
Ab Eb Bb F C G D put in order we get Eb F G Ab Bb C D so the Doo Wop progression in the key of Eb is Eb-Cm-Ab-Bb .
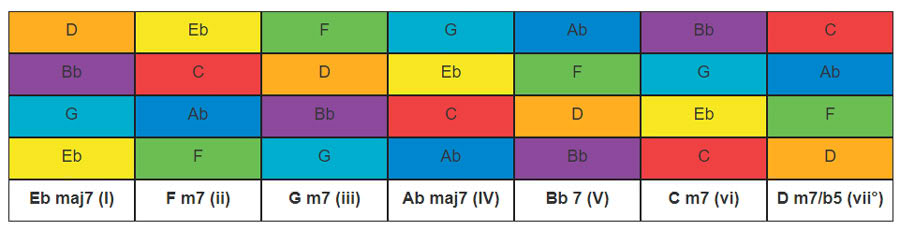
Chords in the Eb key
How to use the Circle of Fifths to change key
Creating songs with chords that belong to the same keys can work, but if we want to be creative, during the song, we can modulate to other keys .
That means our song will have chords that belong to more than one key.
Let's see how to use the Circle of Fifths for key modulation.
Modulate to the relative minor key
And a very quick way to tell the minor corresponding key to each major key is simply the inner circle. The C major key has a relative minor of A , and so on for each note on the CoF. Now this is known as modulating to a relative key.
And that is our next lesson on the CoF.
In music modulating is moving from one key to another, or also put as moving from one tonic (root) to another tonic.
So modulating to the relative key is very simple as it is clearly written out correctly as you look at the CoF.
The modulated relative keys will have the same key signatures.
This change can be difficult to notice for the listener.
Modulate to a parallel key
Now what if we wanted to modulate to a parallel key ? This is another very easy thing to do as the parallel key of a C major is simply a C minor . They can trade places in a song when necessary as they both share the dominate chord.
Modulate to a close key
We can also modulate to another closely related key . To do this we find keys that have similar notes to one another.
This is very simple with the CoF as all we need to do is look at the keys that are beside them .
The key of G and the key of D have many similar notes and thus can make a great and workable change in a song.
A good way to make this change to a closely related key would be using a similar chord that both keys share .
When switching from the key of G to D we can use the D major chord as both keys share this chord making a smooth transition.
You can also modulate by step if you like, but you first have to find the scale of the key you are in.
Once you find it you can modulate by half steps or whole steps if you like.
So moving from C major to C# major would be a half step modulation.
Which follows C major to D major would be a whole-step modulation.
Chain Modulation
There is even a form of chain modulation by using various ideas from above mixed. For example you can start with closely related keys , change to parallel keys , and then add on a relative key change to get these specific key changes in your song:
C G D C Cmin Eb
How to transpose songs
Along with scales, key signatures, chord building, and modulation, we can also use the CoF to transpose our songs .
Now some transposing involves changing the notes so they will fit the pitch of the instrument.
Normal concert pitch is in C, and some woodwinds and brass instruments are in the pitches of Bb, Eb, and F.
However as guitar players we will basically always be in concert pitch so this form of transposition will not be used often.
Instead, we may have to change the key signature of the chords or the progressions.
As we have shown above this can be done in a variety of ways through finding the scales, or modulating.
With the CoF we can accomplish just about any musical task.
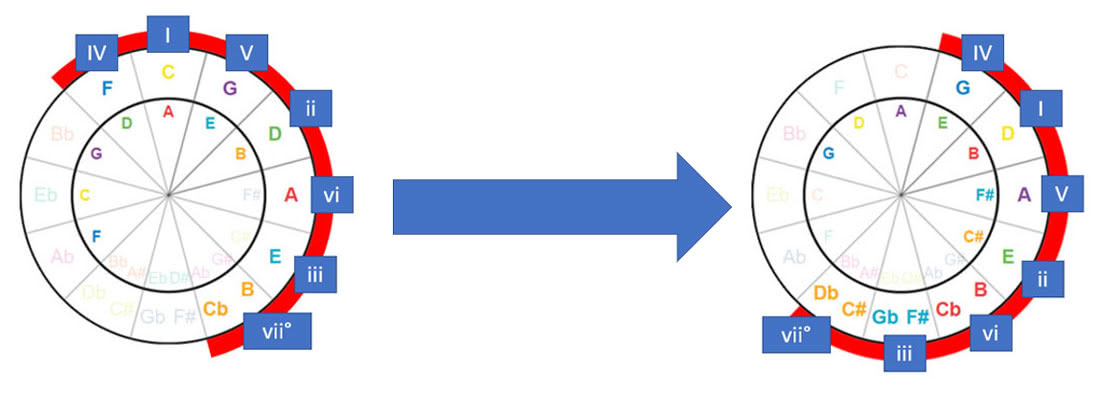
Transposing a song 1 whole step up (from C to D)
The easiest way to transpose a song from one key to another, is to set the root of the new key as degree I in the Circle of Fifths, and find the chords as seen below.
| Scale | I | ii | iii | IV | V | vi | vii° |
|---|---|---|---|---|---|---|---|
| Major | Major | Minor | Minor | Major | Major | Minor | Half-Diminished |
How to construct chords with the Circle Of Fifths
So far we can tell the way in which each note relates and the different key signatures by the CoF, but we can also build entire chords and chord progressions with it.
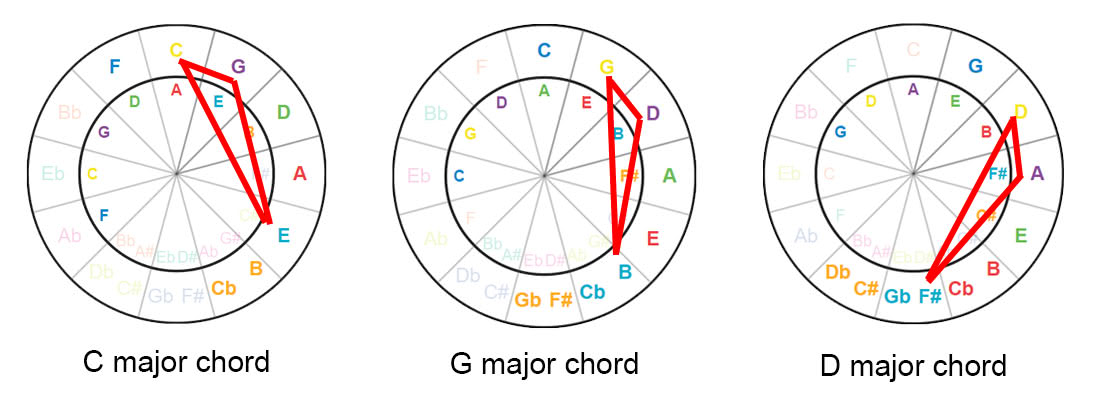
Construct Major Chords
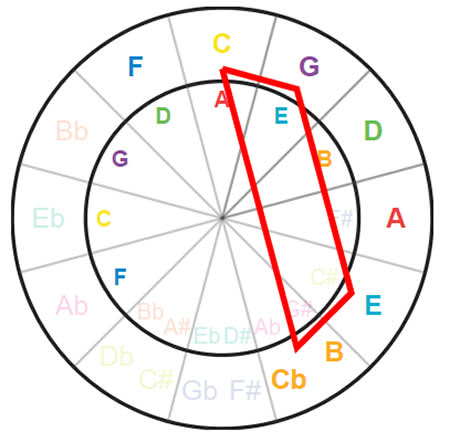
To review, a major chord or triad is made up of the root, third, and fifth.
Now to find a C major chord we take the C scale;
C D E F G A B C
- The root is C
- The third is E
- The fifth is G
If we connect these on the CoF we get a triangle shape.
If you move this exact same shape in any direction you will get other major chords.
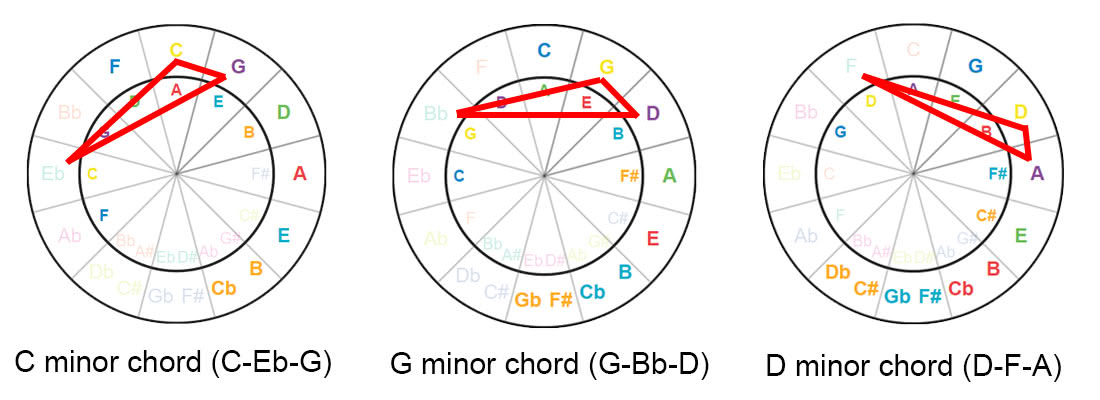
Construct Minor Chords
If you want to find a minor chord like C minor (root, minor 3rd, and fifth);
C Eb G The triangle image is reversed
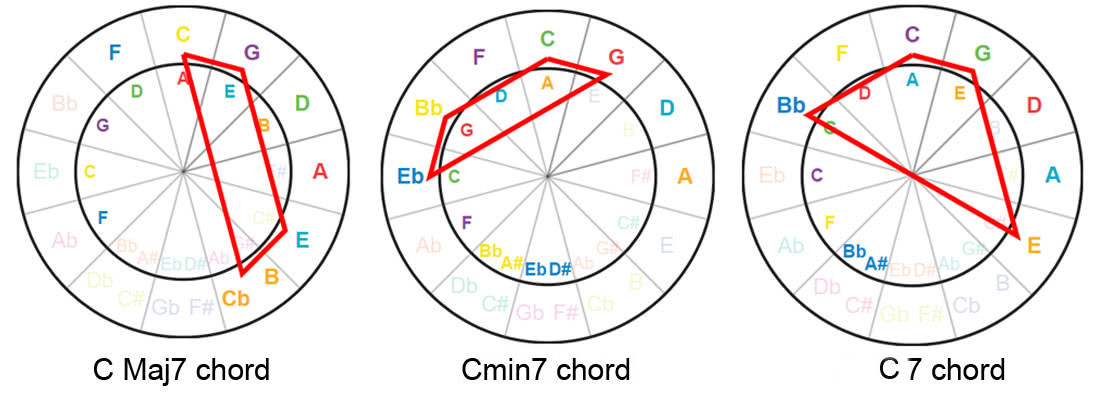
We also have triangle shapes for diminished and augmented chords .
Remember a dim chord is root, minor third, and a flattened fifth. And an augmented chord is the root, major third, and sharp fifth.
As an exercise, try to find those shapes on the circle (the following page shows you all the chords type shapes on the circle of fifths).
If you memorize these shapes you will be able to move the triangles in any direction to find the notes of other chords.
There are also some quadrilateral shapes that can be moved to find various chords.
Construct Seventh Chords
We can extend this concept and construct four chords notes:
- A major seventh chord is made up of the root, major third, perfect fifth, and major seventh.
- A minor seventh is the root, minor third, perfect fifth, and minor seventh.
- The seventh chord is simply made up of the root, major third, perfect fifth, and minor seventh.
Ninth chords do have moveable five-sided shapes, but that can get a little complicated when shifting it.
After time and practice with triangle and trapezoid shapes eventually you will be able to visualize the building blocks of almost every chord on the CoF.
Circle Of Fifths and Modes
Earlier we mentioned finding major scales with the CoF, we kept it easy with only that scale.
However now that you have a better grasp on the CoF let’s take a final look at how to find all other scales or modes .
There are seven modes in western music;
- Ionian: starts on the first note of major scale
- Dorian: starts on second note of major scale
- Phrygian: starts on third note
- Lydian: fourth note
- Mixolydian: fifth note
- Aeolian: sixth note
- Locrian: seventh note
These scales or modes are what give music that certain feel or mood to a song.
An Ionian major scale like we already learned above will have an upbeat and happy sound , while the Aeolian will have a minor and melancholy type feel.
Play each mode to get an idea of how they sound.
And how do we use the CoF to find these modes?
With C at the top of the circle this chart shows us which note will be in which mode.
G comes after C on the CoF, and G is a fifth above C, thus G will be the start of the mixolydian scale !
And of course like all aspects of the CoF we simply rotate these words for each scale . Just like with the shapes, scales, and some modulations from above rotating is the key to the CoF!
If you want to learn more about modes, don't miss our interactive tutorial on modes for guitar
The Circle Of Fourths
While The Circle of Fifths is a well-known tool in music theory, its counterpart, the Circle of Fourths, is equally significant, yet often less highlighted.
The Circle of Fourths is essentially a mirror image of the Circle of Fifths.
While the Circle of Fifths progresses by ascending fifths (e.g., C to G to D), the Circle of Fourths ascends by fourths:
- C
- F
- Bb
- Eb
- Ab
- C#
- F#
- B
- E
- A
- D
- G
- C
Interactive Tool To Learn The Circle of Fifths
As the Circle of Fifths/Wheel of Fifths becomes easier to grasp you will truly see that it is not only useful as a music tool, it is absolutely essential.
If you want your guitar playing and music knowledge to soar to great heights, you will get to know every aspect of the CoF!
To help you study further here is an interactive tool to help you practice the Circle of Fifths. Enjoy!
To stay updated on new tutorials, subscribe to the free newsletter (you'll also get access to the download area with lots of free printable resources)