How to Play A6/9 Chord on Guitar | A Major Sixth Nine Added

A 6/9 position 1 guitar chord diagram

The intervals in this chord are Root, Major Third, Perfect Fifth, Major Sixth, and Major Ninth

Name variations for the A6/9 chord:

  • A Major Sixth Nine Added
  • A 6 Add 9
  • A6/9

The notes in this chord are A, C#, E, F#, and B

Notes of the A 6/9 chord:

AC#EF#B

Tones of the Major Sixth Nine Added chord:

1
b2
2
b3
3
4
b5
5
#5
6
b7
7
8
b9
9
#9
11
#11
13

download this chart in pdf Want to learn everything about chords?

Check Chords Domination out: a unique ebook that shows you finger positions, note names and intervals in the chords (plus a tones fretboard maps)

You'll learn how to play 44 chords types across all the fretboard, with many voicings and fingerings

A Major Sixth Nine Added Guitar Chord Voicings

Chord boxes are sorted from the easiest to the hardest. Learn how to read chord diagrams.

If you have difficulties with bar chord shapes, check the Bar Chords Tips tutorial.

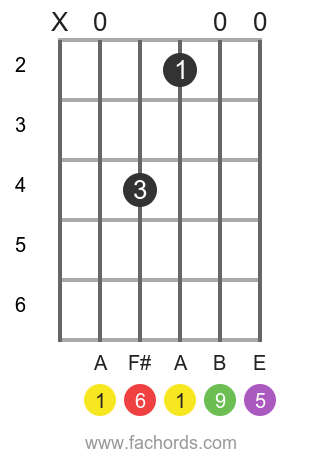
Position 1
Open

A 6/9 position 1 guitar chord diagram

Position 2
Open

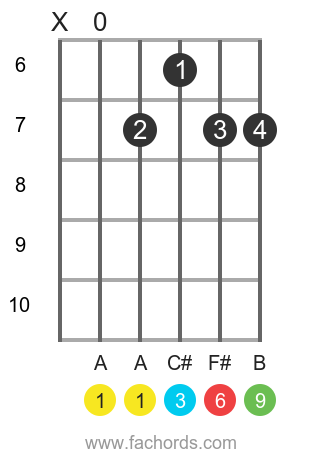
A 6/9 position 3 guitar chord diagram

Position 3
BarreOpen

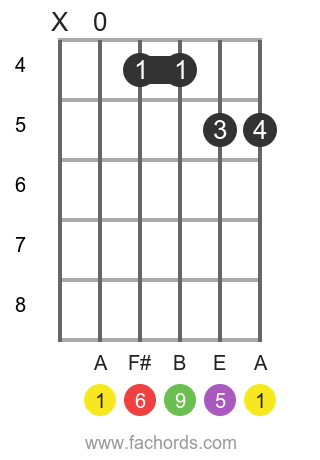
A 6/9 position 2 guitar chord diagram

download this tutorial in pdfWant a printable pdf?
Download the Free Guitar Chords Chart Pdf

Use Fretboard Maps To Build Chords Along All The Fretboard

How to construct the A 6/9 chord on guitar

You can create any fingering you like on any part of the fretboard, just play some of the chord tones shown in the map below. Some shapes will sound good, some less, let your ears decide!

5
9
1
5
6
3
1
5
9
6
9
6
3
1
5
1
3
9
6
1
5
9
3
5
9
6
3
1
6
3
5
9
1
5

These maps show you the tones in a chord all along the fretboard. They are incredibly helpful because allow you to:

  • Create new voicings on the fly, across all the neck
  • Improvise targeting the right notes
  • Unlock the fretboard and expand the CAGED system.

In the new ebook, Chords Domination, you'll find the fretboard tones maps for 44 different qualities of chords. Check it out: